[TOC]

监督学习流程

二元分类

意思就是是猫或者不是猫 这里只是打个比方。

logistic回归

常见的logistic回归就是sigmoid函数套住y=wx+b 公式如下

$$y=\vartheta (\mathbf{W}^\mathrm{T}x+b)$

使得其概率鉴于0-1之间使得sigmoid函数变成这样

$\vartheta (\hat{z} ) = \frac{1} { 1+e^{\hat{z}} }$

损失函数：是衡量单一训练样例的效果

损失函数定义位$\delta (\hat{y} ,y)=\frac{1}{z} (\hat{y}-y)^2$ 就是定义$\hat{y}$和y之间的距离有多近 这里的$\hat{y}$ 就代表了sigmoid(z)函数

但是这个损失函数更好因为e为底 $\delta =-(y(log \hat{y}+(1-y)log(1- \hat{y}))$

损失函数有负号的原因是在逻辑回归中我们需要最小化损失函数，但是由于有个负号并且log函数的单调递增的， 导致其最小化的损失函数就是最大化的logP（y|X）

损失函数又叫做误差函数，用来衡量算法的运行情况，Loss function: L ( $\hat{y}$ , y )

我们通过这个称为 L LL 的损失函数，来衡量预测输出值和实际值有多接近。一般我们用预测值和实际值的平方差或者它们平方差的一半，但是通常在逻辑回归中我们不这么做，因为当我们在学习逻辑回归参数的时候，会发现我们的优化目标不是凸优化，只能找到多个局部最优值，梯度下降法很可能找不到全局最优值，虽然平方差是一个不错的损失函数，但是我们在逻辑回归模型中会定义另外一个损失函数。

我们在逻辑回归中用到的损失函数是：
$ J=-(y(log \hat{y}+(1-y)log(1- \hat{y}))$

成本函数:衡量w和b的效果

成本函数是 $J(\delta,b)=\frac{1}{m} \sum_{1}^{m} \delta (\hat{y} ,y) = -\frac{1}{m} \sum_{1}^{m} [(-y^{i}(log\hat{y}^{i}+(1-y^{i})log(1- \hat{y}^{i} ))]$ y代表1或0 举个是否鉴别猫的例子

1/m是可以加或者不加的 但是加的原因是对可以对单个成本进行估计，也就是适当的缩放损失函数。

梯度下降法：找到最小的成本函数

1694484928365

找到最低点 令$w=w-\alpha \frac{\mathrm{d} j(w)}{\mathrm{d} w} $

找到极小值 意思就是牛顿迭代， 举个例子w在极小值（最低点）右边 此时斜率>0 但是$\alpha \frac{\mathrm{d} j(w)}{\mathrm{d} w}$>0

这时候w就会变小 左边就同理

同理 找成本函数的参数b的时候$b=b-\alpha \frac{\mathrm{d} j(b)}{\mathrm{d} b} $

计算梯度

image-20230912104555026a

image-20230912150316908

向量化：加速计算，摆脱显示for循环语句

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import time//此案例为比较向量化运算和非向量化运算之间的速度
a = np.random.rand(1000000)
b = np.random.rand(1000000)

tic = time.time()
c = np.dot(a,b)
toc = time .time()


print(c)
print("vector :" + str(1000*(toc-tic)) + "ms")

c=0;
tic = time.time()

for i in range(1000000):
    c+= a[i]*b[i]
toc = time.time()
print(c)
print("for loop"+ str(1000*(toc-tic)) + "ms")

向量化的logistic回归

image-20230912170514411

将z写成向量乘法的形式用np内置库进行运算从而摆脱for循环

python的广播机制：意思就是将一个向量+上一个常数后 该常熟就自动被扩展成与该向量行和列匹配的向量

如

image-20230912171046265

等于

image-20230912171059528

dz 和dw的计算脱离for循环变成

image-20230912172407404

非向量化的 logic回归版本：image-20230912172526590

向量化后简化的版本：

image-20230912173545392

ps: python 广播机制举例：3x4矩阵+1x4矩阵 1x4矩阵会自动扩充成 3x4矩阵

image-20230913152604028

注：在使用数据的时候尽量不要使用矩阵秩为1的矩阵来操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#实现sigmoid函数

def sigmoid(x):
   s= 1 /(np.exp(-x) +1)#np.exp（x）适用于任何np.array x并将指数函数应用于每个坐标
    return s
def sigmoid_derivative(x):
    s= sigmoid(x)
    ds = s*(1-s)
    return ds

#实现输入采用维度为(length, height, 3)的输入，并返回维度为(length*height*3, 1)的向量。
def image2vector(image):
    v = image.reshape((image.shape[0]*image.shape[1]*image.shape[2]),1)
    return v

image = np.array([[[ 0.67826139,  0.29380381],
        [ 0.90714982,  0.52835647],
        [ 0.4215251 ,  0.45017551]],
         [[ 0.92814219,  0.96677647],
    [ 0.85304703,  0.52351845],
    [ 0.19981397,  0.27417313]],

   [[ 0.60659855,  0.00533165],
    [ 0.10820313,  0.49978937],
    [ 0.34144279,  0.94630077]]])
    print ("image2vector(image) = " + str(image2vector(image)))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
x1 = [9, 2, 5, 0, 0, 7, 5, 0, 0, 0, 9, 2, 5, 0, 0]
x2 = [9, 2, 2, 9, 0, 9, 2, 5, 0, 0, 9, 2, 5, 0, 0]

### VECTORIZED DOT PRODUCT OF VECTORS ###
tic = time.process_time()
dot = np.dot(x1,x2)
toc = time.process_time()
print ("dot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### VECTORIZED OUTER PRODUCT ###
tic = time.process_time()
outer = np.outer(x1,x2)
toc = time.process_time()
print ("outer = " + str(outer) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### VECTORIZED ELEMENTWISE MULTIPLICATION ###
tic = time.process_time()
mul = np.multiply(x1,x2)
toc = time.process_time()
print ("elementwise multiplication = " + str(mul) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")

### VECTORIZED GENERAL DOT PRODUCT ###
tic = time.process_time()
dot = np.dot(W,x1)
toc = time.process_time()
print ("gdot = " + str(dot) + "\n ----- Computation time = " + str(1000*(toc - tic)) + "ms")
dot = 278
 ----- Computation time = 0.0ms
outer = [[81 18 18 81  0 81 18 45  0  0 81 18 45  0  0]
 [18  4  4 18  0 18  4 10  0  0 18  4 10  0  0]
 [45 10 10 45  0 45 10 25  0  0 45 10 25  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [63 14 14 63  0 63 14 35  0  0 63 14 35  0  0]
 [45 10 10 45  0 45 10 25  0  0 45 10 25  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [81 18 18 81  0 81 18 45  0  0 81 18 45  0  0]
 [18  4  4 18  0 18  4 10  0  0 18  4 10  0  0]
 [45 10 10 45  0 45 10 25  0  0 45 10 25  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]
 [ 0  0  0  0  0  0  0  0  0  0  0  0  0  0  0]]
 ----- Computation time = 0.0ms
elementwise multiplication = [81  4 10  0  0 63 10  0  0  0 81  4 25  0  0]
 ----- Computation time = 0.0ms
gdot = [ 21.57937154  22.58814194  13.70092277]
 ----- Computation time = 0.0ms

总的来说还是根据sgmoid公式来进行概率的预测

先初始化w和b 然后通过梯度下降来优化获得更好的w和b

然后通过预测函数来进行概率预测

总结逻辑回归需要先算

image-20230917193629126

然后算 $\vartheta (\hat{z} )$ 也就是sigmoid(z)

image-20230917103418475

什么是神经网络

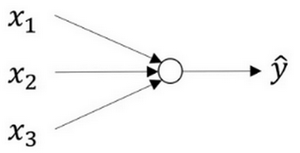
如上图，类比与监督学习的逻辑回归来说 神经网络就是多个

逻辑回归叠加的结果，叠加后到达下一层。

img

image-20230917105353093

首先你需要输入特征 x ，参数 w 和b ，通过这些你就可以计算出 z ，

image-20230917105433820

接下来使用就可以计算出 a aa 。我们将的符号换为表示输出 y ^ → a = σ ( z ) \hat{y}\rightarrow a=\sigma(z)
y
^

→a=σ(z) ,然后可以计算出loss function L ( a , y ) L(a,y)L(a,y)

神经网络看起来是如下这个样子。正如我之前已经提到过，你可以把许多sigmoid单元堆叠起来形成一个神经网络。对于图3.1.1中的节点，它包含了之前讲的计算的两个步骤：首先通过公式计算出值z ，然后通过 σ ( z ) \sigma(z)σ(z) 计算值 a 。

img

这个神经网络对于三个节点 首先计算第一层网络中的各个相关的数$z^{[1]} $

，接着计算$a^{[1]}$接着计算下一层网络 等等 意思就是不同层使用$^{[m]}$代表第m层中节点相关的数，这些节点的集合被称为第m层网络。

这样可以保证$^{[m]}$不会和我们之前标识单个训练样本的$^{(i)}$混淆 公式3.3如下

image-20230917110321224

类似逻辑回归，在计算后需要使用计算，接下来你需要使用另外一个线性方程对应的参数计算 $z^{[2]}$然后计算$a^{[2]}$

，此时 $a^{[2]}$ 就是整个神经网络最终的输出，用$\hat{y}$

image-20230917110729088

神经网络表示

img

我们有输入特征 x 1 、 x 2 、 x 3 x_1、x_2、x_3x
1

、x
2

、x
3

，它们被竖直地堆叠起来，这叫做神经网络的输入层(Input Layer)。它包含了神经网络的输入；然后这里有另外一层我们称之为隐藏层(Hidden Layer)（图3.2.1的四个结点）。待会儿我会回过头来讲解术语”隐藏”的意义；在本例中最后一层只由一个结点构成，而这个只有一个结点的层被称为输出层(Output Layer)，它负责产生预测值。解释隐藏层的含义：在一个神经网络中，当你使用监督学习训练它的时候，训练集包含了输入 x xx 也包含了目标输出 y yy ，所以术语隐藏层的含义是在训练集中，这些中间结点的准确值我们是不知道到的，也就是说你看不见它们在训练集中应具有的值。你能看见输入的值，你也能看见输出的值，但是隐藏层中的东西，在训练集中你是无法看到的。所以这也解释了词语隐藏层，只是表示你无法在训练集中看到他们。

现在讲层数

就像我们之前用向量 x 表示输入特征。这里有个可代替的记号 $ a^{[0]}$可以用来表示输入特征。 a 表示激活的意思，它意味着网络中不同层的值会传递到它们后面的层中，输入层将 x 传递给隐藏层，所以我们将输入层的激活值称为 $a^{[0]}$ 下一层即隐藏层也同样会产生一些激活值，那么我将其记作 $a^{[1]}$ ，所以具体地，这里的第一个单元或结点我们将其表示为 $a_{1}^{[1]}$ ，第二个结点的值我们记为 $ a_{2}^{[1]}$ 以此类推。所以这里的是一个四维的向量如果写成Python代码，那么它是一个规模为4x1的矩阵或一个大小为4的列向量，如下公式，它是四维的，因为在本例中，我们有四个结点或者单元，或者称为四个隐藏层单元

image-20230917112841893

最后输出层将产生某个数值 a ，它只是一个单独的实数，所以 $ \hat{y}$ 的值将取为 $a^{[2]}$ 。这与逻辑回归很相似，在逻辑回归中，我们有 y$^ \hat{y}$ 直接等于 a ，在逻辑回归中我们只有一个输出层，所以我们没有用带方括号的上标。但是在神经网络中，我们将使用这种带上标的形式来明确地指出这些值来自于哪一层，有趣的是在约定俗成的符号传统中，在这里你所看到的这个例子，只能叫做一个两层的神经网络（如下图）。原因是当我们计算网络的层数时，输入层是不算入总层数内，所以隐藏层是第一层，输出层是第二层。第二个惯例是我们将输入层称为第零层，所以在技术上，这仍然是一个三层的神经网络，因为这里有输入层、隐藏层，还有输出层。但是在传统的符号使用中，如果你阅读研究论文或者在这门课中，你会看到人们将这个神经网络称为一个两层的神经网络，因为我们不将输入层看作一个标准的层。同理w和b加上上标也是对应不同层的不同参数类似$ w^{[1]}$ 和$b^{[1]}$

image-20230917113049572

接下来是对各个层的神经单元进行的公式举例如图image-20230917191923227

当然这个用四个for循环效率太低 可以使之向量化从而减轻运算量

如

image-20230917192457917

上面相乘是 4x3矩阵 乘以 3x1的矩阵在加一个4x1的矩阵从而得到$z^{[1]}$

w一开始是3x4的

接下来是向量化

注意$a^{1}$ 这里的i标识第几个样本 1标识第一层神经网路

m个样本要计算实现这四个公式

image-20230917195503865

接下来就是将向量横向堆积的过程image-20230917201131159

这里具体就是将${z^{1},z^{1}…….z^{1}}$进行堆积形成$Z^{[1]}$然后通过$\vartheta (z^{1}),\vartheta (z^{1})…….\vartheta (z^{1})$向量横向排列形成$A^{[a]}$

像这样

image-20230917201739141

image-20230917201941190

经过此处导可以得出$z^{[1]} = w^{[1]}X + b^{[1]}$

如下图

image-20230917202420741

激活函数

这里有sigmoid函数和tanh函数image-20230917202959386

image-20230917203115556

其实tanh函数是sigmoid函数平移的结果

tanh函数更好用

sigmoid函数和tanh函数两者共同的缺点是，在 z 特别大或者特别小的情况下，导数的梯度或者函数的斜率会变得特别小，最后就会接近于0，导致降低梯度下降的速度。

机械学习中还有这个函数ReLu修正线性单元

image-20230917203802613

选择激活函数有技巧：

如果输出是0、1值（二分类问题），则输出层选择sigmoid函数，然后其它的所有单元都选择Relu函数。

这是很多激活函数的默认选择，如果在隐藏层上不确定使用哪个激活函数，那么通常会使用Relu激活函数。有时，也会使用tanh激活函数，但Relu的一个优点是：当 z zz 是负值的时候，导数等于0。

这里也有另一个版本的Relu被称为Leaky Relu。

当 z zz 是负值时，这个函数的值不是等于0，而是轻微的倾斜，如图。

这个函数通常比Relu激活函数效果要好，尽管在实际中Leaky ReLu使用的并不多。

img

为什么要用非线性激活函数？

实证明，如果你使用线性激活函数或者没有使用一个激活函数，那么无论你的神经网络有多少层一直在做的只是计算线性函数，所以不如直接去掉全部隐藏层。在我们的简明案例中，事实证明如果你在隐藏层用线性激活函数，在输出层用sigmoid函数，那么这个模型的复杂度和没有任何隐藏层的标准Logistic回归是一样的，如果你愿意的话，可以证明一下。

在这里线性隐层一点用也没有，因为这两个线性函数的组合本身就是线性函数，所以除非你引入非线性，否则你无法计算更有趣的函数，即使你的网络层数再多也不行；只有一个地方可以使用线性激活函数——— g ( z ) = z ，就是你在做机器学习中的回归问题。 y yy 是一个实数，举个例子，比如你想预测房地产价格， y 就不是二分类任务0或1，而是一个实数，从0到正无穷。如果 y y是个实数，那么在输出层用线性激活函数也许可行，你的输出也是一个实数，从负无穷到正无穷。

总而言之，不能在隐藏层用线性激活函数，可以用ReLU或者tanh或者leaky ReLU或者其他的非线性激活函数，唯一可以用线性激活函数的通常就是输出层；除了这种情况，会在隐层用线性函数的，除了一些特殊情况，比如与压缩有关的，那方面在这里将不深入讨论。在这之外，在隐层使用线性激活函数非常少见。因为房价都是非负数，所以我们也可以在输出层使用ReLU函数这样你的 $\hat{y}$ 都大于等于0。

正向传播和反向传播的区别3.9 神经网络的梯度下降法-深度学习-Stanford吴恩达教授_吴恩达梯度下降法的公式_Zhao-Jichao的博客-CSDN博客

为什么要反向传播？

反向传播就是为了实现最优化，省去了重复的求导步骤

这里不详细讨论方向传播算法的原理了，简单来说这种方法利用了函数求导的链式法则，从输出层到输入层逐层计算模型参数的梯度值，只要模型中每个计算都能求导，那么这种方法就没问题。可以看到按照这个方向计算梯度，各个神经单元只计算了一次，没有重复计算。这个计算方向能够高效的根本原因是，在计算梯度时前面的单元是依赖后面的单元的计算，而“从后向前”的计算顺序正好“解耦”了这种依赖关系，先算后面的单元，并且记住后面单元的梯度值，计算前面单元之就能充分利用已经计算出来的结果，避免了重复计算。

深度学习——反向传播（Backpropagation）_南方惆怅客的博客-CSDN博客

首先，你需要正向传播，来计算z对w的偏导，进而求出sigmoid’(z)是多少。然后，根据输出层输出的数据进行反向传播，计算出l对z的偏导是多少，最后，代入到公式0当中，即可求出l对w的偏导是多少。注意，这个偏导，其实反应的就是梯度。然后我们利用梯度下降等方法，对这个w不断进行迭代（也就是权值优化的过程），使得损失函数越来越小，整体模型也越来越接近于真实值。

3.10 直观理解反向传播-深度学习-Stanford吴恩达教授_Zhao-Jichao的博客-CSDN博客

随机初始化

一句话就是初始化不要全部为0，要随机初始化

如果 w 很大，那么你很可能最终停在（甚至在训练刚刚开始的时候） z z很大的值，这会造成tanh/Sigmoid激活函数饱和在龟速的学习上，如果你没有sigmoid/tanh激活函数在你整个的神经网络里，就不成问题。但如果你做二分类并且你的输出单元是Sigmoid函数，那么你不会想让初始参数太大，因此这就是为什么乘上0.01或者其他一些小数是合理的尝试。对于 $ w^{[2]}$ 一样，就是np.random.randn((1,2))，我猜会是乘以0.01。

事实上有时有比0.01更好的常数，当你训练一个只有一层隐藏层的网络时（这是相对浅的神经网络，没有太多的隐藏层），设为0.01可能也可以。但当你训练一个非常非常深的神经网络，你可能要试试0.01以外的常数。下一节课我们会讨论怎么并且何时去选择一个不同于0.01的常数，但是无论如何它通常都会是个相对小的数。

image-20230918105011317

就比如这个图 假如给的w参数很大 那么生成的z就很大 z 很大就会导致激活函数处在末端 也就是图中箭头位置

那么从图中看出该出斜率比较平缓，从而导致计算反向梯度的时候会很慢。

正向传播 反向传播

image-20230919170349561

向量化版本

image-20230919170642156

意思就是i先算出$da^{[l]}$

然后得出$da^{[l-1]}$,$dw^{[l]}$,$db^{[l]}$

深度神经网络学习中 正向传播可能不同隐藏层有着不同的激活函数 然后得到损失函数后 在进行迭代 反向传播

如下图

image-20230919171014362

计算正向传播的矩阵维度会有一个规律

核对矩阵维数

w 的维度是（下一层的维数，前一层的维数），即 $w^{[l]}:(n^{[l]},n^{[l-1]})$

b 的维度是（下一层的维数，1） $b^{[l]}:(n^{[l]},1)$

同理 $dw^{[l]}:(n^{[l]},n^{[l-1]})$

$db^{[l]}:(n^{[l]},1)$

img

单个数据样本$W^{[l]}：(n^{[1]},1)$时候 矩阵乘法很容易理解$z^{[1]} = w^{[1]}x + b^{1}$ $z^{[2]} = w^{[2]}a^{[1]} + b^{2}$

此时$a^{[2]} = g(z^{[1]})$ 同理将多个数据样本平铺起来的时候变成平铺的向量

变成如下图

img